Recovering RSA-512 Key Pair with Distributed CADO-NFS
Intro#
RSA is currently the most widely used public-key cryptosystem in the world. In public-key cryptography, there are two kinds of keys: private keys and public keys. Private keys are generated by some algorithm and need to be kept secret by the operator. Public keys are directly derived from private keys and can be published publicly anywhere. A public key together with the private key which it’s derived from is called a key pair.
The key size of a key pair in RSA refers to the expected length (in bits) of the generated RSA modulus. It determines the overall security of the key pair. As of August 2023, the recommended least key size is 2048 bits. Unfortunately, some developers don’t take best practices for security consideration and are still using 512-bit RSA keys.
This article demonstrates recovery of the private key (PKCS#1 / PKCS#8 format) from an already known RSA-512 public key by factorizing RSA modulus with CADO-NFS.
Disclaimer: This article is intended for educational purposes only. The author does not condone or encourage any illegal activities. The information provided in this article is for informational purposes only and should not be used for any illegal activities. The author is not responsible for any misuse of the information provided in this article.
Review on RSA#
Formalization#
-
Choose two primes $p, q$ and $N:=pq$ is the modulus for the key pair.
-
Compute $\lambda(N)=\lambda(pq)=\operatorname{lcm}(p-1,q-1)$.
Here $\lambda(n)$ is Carmichael’s totient function, defined as $\eqref{carmichael}$.
$$ \begin{equation} \lambda(n):=\min\{m>0: \forall a \in{}\mathbf{R}^*_n, a^m\equiv 1\pmod n\}\label{carmichael} \end{equation} $$where $\mathbf{R}^*_{n}{}:= \{i\in{}\mathbf{R}_n: \gcd(n, i) = 1\}$ is the reduced residue system modulo $n$.
Many textbooks are instead using Euler’s totient function $\varphi(n)$. This does not affect the correctness.
-
Choose a public exponent $e\neq 1$ so that $e\in{}\mathbf{R}^*_{\lambda(n)}$, namely $e$ is coprime to $\lambda(n)$.
-
Compute the private exponent $d:\equiv e^{-1}\pmod{\lambda(n)}$.
-
For end-to-end encryption: the encryptor $E(m):\equiv m^e\pmod N$ and the decryptor $D(m):\equiv m^d\pmod N$.
-
For signing purposes: the signer $\DeclareMathOperator*{\concat}{\Vert} S(m):=D( \operatorname{hash}(m))$
I am not giving any proof of correctness here since it’s a bit off-topic, but you can see the proof written by Stein in his book Elementary Number Theory: Primes, Congruences, and Secrets here.
The formalization here is quite pedantic, there are much more restrictions in real life implementations, like the moderate distance between $p,q$, requirement on $e>2$ and the usage of fixed value $e:=65537$ in common libraries.
Components in Real Life#
The tuple $(p, q, e)$ can uniquely determines an RSA key pair, this is quite obvious from the steps above. In theory a private key COULD be $(p, q, d)$ and the derived public key is thus $(N, e)=(pq, e)$. It’s also feasible to take $(p, q, e)$ as the private key tuple.
From mathematical context, the form of components is not unique but they are equivalent. So what stuff are actually stored in modern private key files? More specifically, what are the real components stored in PKCS#1 / PKCS#8? In fact, modern private key formats store components more than necessary, for space–time tradeoff.
Private Key Components#
Let’s generate a random key and inspect its components via OpenSSL:
|
|
By default, openssl genrsa will generate keys in PKCS#8 format. This private key contains:
- modulus corresponds to $N:=pq$
- publicExponent corresponds to $e$, OpenSSL always uses fixed value $e:=65537$ when generating new keys
- privateExponent corresponds to $d:\equiv e^{-1}\pmod{\lambda(n)}$
- prime1 and prime2 correspond to $p$ and $q$
But who’s giving exponent1, exponent2, coefficient?
Sped-up Exponentiation#
The point of these three unknown components is to make the decryptor
$$ D(m):\equiv m^d\pmod N $$and the signer $S(m)$ faster by Chinese remainder theorem.
In general this is actually an algorithm to compute modulus exponentiation for big numbers. Since the multiplication for big ones is not trivial operation (Karatsuba, FFT etc.) thus cannot be treated as $O(1)$, it is commonly implemented by some library.
Computing $m^d\pmod N$ is equivalent to solving $\eqref{crt-1}$, which is trivially solvable,
$$ \begin{equation} x\equiv m^d\pmod{pq}\label{crt-1} \end{equation} $$Since $p,q$ are primes, they are obviously coprime i.e. $\gcd(p,q)=1$. Justified by CRT, equation $\eqref{crt-1}$ can be rewritten equivalently into a system $\eqref{crt-2}$,
$$ \begin{equation} \left\{ \begin{aligned} x&\equiv m^d\pmod{p} \\ x&\equiv m^d\pmod{q} \end{aligned} \right.\label{crt-2} \end{equation} $$Now the modulus $N$ has been halved (in digits) into $p,q$, hence the exponential part $d$ is able to be reduced.
For a prime, its Carmichael’s $\lambda$ is equal to Euler’s $\varphi$, which states
$$ \lambda(p)=\varphi(p)=p-1,\lambda(q)=\varphi(q)=q-1 $$Let $d_p:\equiv d\pmod{\lambda(p)}$ and $d_q:\equiv d\pmod{\lambda(q)}$, this states $k_p,k_q\in\mathbb{Z}$ exist so that
$$ d=k_p\lambda(p)+d_p=k_q\lambda(q)+d_q, $$By applying Euler’s theorem, the exponential part is reduced to $\eqref{crt-3}$
$$ \begin{equation} \left\{ \begin{aligned} x&\equiv m^d\equiv m^{k_p\lambda(p)+d_p}\equiv m^{d_p}\pmod{p} \\ x&\equiv m^d\equiv m^{k_q\lambda(q)+d_q}\equiv m^{d_q}\pmod{q} \end{aligned} \right.\label{crt-3} \end{equation} $$The smaller exponents $d_p$ and $d_q$ are called exponent1 and exponent2 in the component list above, they are precomputed in the private key.
By applying CRT algorithm here, the solution is $\eqref{crt-4}$
$$ \begin{equation} x\equiv m^{d_q} + q^*(m^{d_p}-m^{d_q})q \pmod{pq}\label{crt-4} \end{equation} $$where $q^*:\equiv q^{-1} \pmod p$, and is called coefficient in the component list above.
In conclusion, those extra components are generally called CRT components:
- exponent1 (paired with prime1 $p$) is $d_p:\equiv d\pmod{\lambda(p)}$, where $\lambda(p)=p-1$
- exponent2 (paired with prime2 $q$) is $d_q:\equiv d\pmod{\lambda(q)}$, where $\lambda(q)=q-1$
- coefficient is $q^*:\equiv q^{-1} \pmod p$
Public Key Components#
Derive the public key from previously generated private key, and inspect its components:
|
|
Public keys are simpler, and the list shows exactly the tuple $(N,e)$.
Recover Key Pair#
The trapdoor in RSA ensures that an attacker cannot recover the private key easily from a public key, unless they do know the factorization of the modulus i.e. $N=pq$. Looking up the factorization on factordb is always a good idea, but the successful cases are rare in real life.
If someone is using RSA-512, the attacker can spend less than a week to factorize the modulus stored in the public key with CADO-NFS software suite, which implements NFS algorithm.
Distributed Factorization#
CADO-NFS supports a central server for distributed computation. Here are some additional tips:
-
Use same Linux distro OR same Docker image on the server and clients, if distributed
Otherwise, you probably need to struggle with
glibcversion compatibility issues. -
Pay attention to the output after CADO-NFS server starts up, which will contain a command for restoring progress, this is quite useful if the server accidentally exits.
Prerequisites#
-
Aside from common toolchains,
cmakeandlibgmp3-devare required to build CADO-NFS. -
Download CADO-NFS source tarball, extract and enter the directory.
-
Run
make -j8. (adjust the job number to fit your workload) -
./cado-nfs.pyand./cado-nfs-client.pyare ready to use. -
Get modulus and public exponent from public key
pub.pem, some digits are redacted.1 2 3 4 5 6 7 8 9 10 11$ openssl pkey -pubin -in pub.pem -noout -text Public-Key: (512 bit) Modulus: 00:bc:dd:6e:bc:57:ae:a2:be:7d:ad:70:8f:71:0a: 80:86:3b:c5:18:f7:ab:4d:5e:bd:a5:64:b2:65:d2: 7c:d9:4c:5e:e3:c3:bc:33:b7:60:30:98:bd:6d:c4: **:**:**:**:**:**:**:**:**:**:**:**:**:**:**: **:**:**:**:** Exponent: 65537 (0x10001) $ openssl rsa -pubin -in public.pem -noout -modulus Modulus=BCDD6EBC57AEA2BE7DAD708F710A80863BC518F7AB4D5EBDA564B265D27CD94C5EE3C3BC33B7603098BD6DC4****************REDACTED****************You just need to convert the hexadecimal form into decimal number, for example evaluate it directly in Python
1 2$ python -c "print(0xBCDD6EBC57AEA2BE7DAD708F710A80863BC518F7AB4D5EBDA564B265D27CD94C5EE3C3BC33B7603098BD6DC4****************REDACTED****************)" 9891661152720289911993780388856560399924301310754393756699908896661301299157403390541217712185535804***********************REDACTED***********************
Server#
|
|
Clients#
|
|
Change server to your server address and modify --override -t 8 to override the thread number on different clients.
Result#
The final output will be just two primes, as shown below.
95488332303787905388806934005632272891519544646395*************************** 103590259815731432651796987187054092306262180182970***************************
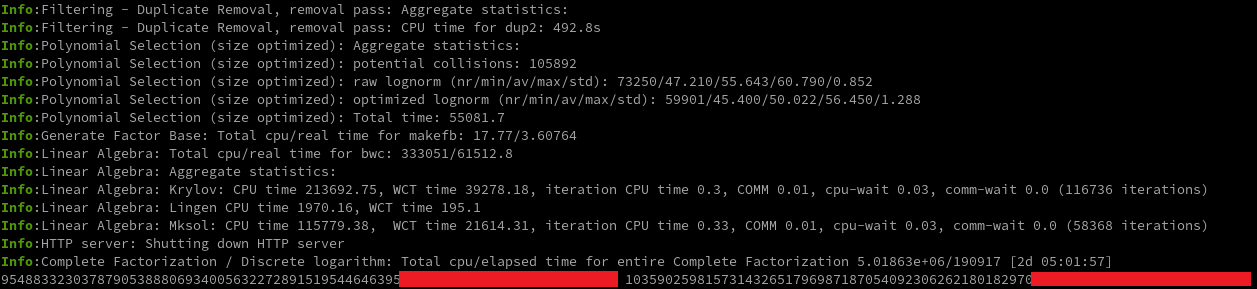
Factorization Result
Construct Private Key#
To construct a private key with CRT components easily, I recommend to use rsatool.py.
You’ll need to clone the repository and run pip install . in its directory first.
|
|
Now the private key is recovered and ready to use. This tool creates keys in PKCS#1 format. To convert it to PKCS#8 format, simply run
|
|