分布式 CADO-NFS 还原 RSA-512 密钥

密码学 rsa cado-nfs
有 1 种语言版本可以阅读 English

简介#

RSA 是目前全世界使用最广泛的公钥密码体系. 公钥密码体系中，有两类密钥：私钥与公钥. 私钥是由算法生成的，并由操作者妥善保管. 公钥是从私钥推导而出的，可以公开发布给任何人. 公钥及其对应的私钥为一对密钥.

RSA 密钥的大小指的是 RSA 加密或解密运算中模的长度（按 bit 计算），它决定了密钥的整体安全性. 截至 2023 年 8 月，推荐的最小模长为 2048 位. 不过总有开发者罔顾安全性最佳实践，仍然在实际项目中使用 512 位 RSA 密钥.

本文将演示如何使用 CADO-NFS 将 RSA-512 的公钥恢复成 PKCS#1 / PKCS#8 格式的私钥.

免责声明: 本文仅供教育目的，作者不支持或鼓励任何非法活动. 本文提供的信息仅供参考，不应用于任何非法活动. 作者不对滥用本文提供的信息所造成的后果负责.

RSA 小复习#

形式化表述#

  • 选择两个素数 p,q 将 N:=pq 作为密钥的模.

  • 计算 λ(N)=λ(pq)=lcm(p−1,q−1).

    这里 λ(n) is Carmichael 函数, 定义见 (1).

    λ(n):=min{m>0:∀a∈R∗n,am≡1(modn)}

    其中 R∗n:={i∈Rn:gcd(n,i)=1} 是模 n 的简化剩余系.

    许多教科书使用的是 Euler 函数 φ(n)，这不影响算法的正确性.

  • 选择一个公开指数 e≠1 使得 e∈R∗λ(n)，即 e 与 λ(n) 互素.

  • 计算私有指数 d:≡e−1(modλ(n)).

  • 对于端到端加密，加密机定义为 E(m):≡me(modN) 而解密机定义为 D(m):≡md(modN).

  • 签名机定义为 S(m):=D(hash(m))

此处并不打算给出任何关于 RSA 正确性的证明，感兴趣的读者可以阅读 William Stein 在他的著作 Elementary Number Theory: Primes, Congruences, and Secrets 中的证明.

这里的形式化表述比较学院派，生活中的算法实现有更多苛刻的安全条件，例如 p,q 间的距离要适度, 公开指数至少满足 e>2 的要求，并且密码学函数库往往用 e:=65537 这一固定值作为公开指数，更多实践可参考此处.

现实中的 RSA 成分#

从上面的形式化表述中，显然 3 元组 (p,q,e) 能够唯一地决定一对 RSA 密钥. 理论上，一个 RSA 私钥成分的表示可以用 (p,q,d) 而其对应的公钥成分就是 (N,e)=(pq,e). 当然了，使用 (p,q,e) 也能作为 RSA 私钥成分的一种表示方式.

数学上来看，私钥的成分表示方式其实并不唯一，那么在现代的私钥文件中究竟存储了什么东西呢？换句话说，在 PKCS#1 / PKCS#8 这些私钥格式中，究竟存储了什么样的成分？事实上现代私钥格式中，为了权衡算法的时空性能，存储了更多的成分.

私钥成分#

让 OpenSSL 给我们生成一个 RSA-512 私钥，并列出其成分：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

$ openssl genrsa 512 | tee sample.key | openssl pkey -noout -text
Private-Key: (512 bit, 2 primes)
modulus:
    00:e8:b1:ea:27:bc:3a:a6:9f:53:48:24:9c:5a:9d:
    9e:64:af:12:3e:ae:db:46:f0:4d:99:55:61:fd:c2:
    c8:45:35:25:05:e6:7b:37:c0:cc:92:7a:45:c0:5b:
    01:a3:4c:4e:87:5b:70:48:62:05:2a:6e:c2:3a:6a:
    f0:07:92:61:ad
publicExponent: 65537 (0x10001)
privateExponent:
    00:ca:ec:5c:86:ca:5f:5b:6f:15:f1:93:fb:c6:0a:
    2e:57:1f:55:89:d4:72:e5:2a:2a:81:cd:33:e7:58:
    35:ce:23:20:af:2c:e6:fd:39:4e:2f:a6:be:23:23:
    7f:e3:d2:f1:81:98:ef:48:91:a3:94:68:04:c6:a6:
    d3:49:df:a8:01
prime1:
    00:f6:a8:8b:b4:cb:45:0f:d8:b9:6b:de:32:31:87:
    c1:98:05:6d:d0:07:3d:c0:c0:8d:3d:5c:c1:1a:3a:
    64:7d:45
prime2:
    00:f1:81:fc:ee:f1:5b:01:58:0c:0a:92:e2:fe:84:
    17:f2:9d:f9:bb:e9:6a:4d:fd:77:56:37:32:76:68:
    54:15:49
exponent1:
    00:c2:d9:14:3b:c6:d3:90:98:18:a9:c0:86:10:20:
    78:eb:19:66:cd:0d:db:57:78:04:5a:f3:f9:cb:39:
    53:86:ad
exponent2:
    32:ff:5e:f8:d9:f0:7c:ad:2a:05:c5:94:b7:68:0f:
    62:85:27:6a:1d:d4:fb:d9:0d:2d:20:84:c0:6a:31:
    6f:39
coefficient:
    00:bf:63:63:7b:71:73:ab:59:66:7d:2e:6f:eb:8a:
    e3:88:a1:10:cb:db:5f:fb:d4:83:31:52:2d:97:6c:
    38:29:50

默认情况下 openssl genrsa 会生成 PKCS#8 的格式，上面的私钥中包含了：

  • modulus 对应了 RSA 的模 N:=pq
  • publicExponent 对应了公开指数 e, OpenSSL 在生成私钥时总使用固定值 e:=65537
  • privateExponent 对应了私有指数 d:≡e−1(modλ(n))
  • prime1 和 prime2 对应了 p 和 q

那么 exponent1, exponent2, coefficient 究竟是什么东西?

CRT 改进的快速幂#

对解密机 D(m):≡md(modN) 与签名机 S(m) 用中国剩余定理（CRT）变换后，会出现上面额外的成分，这是一种能够加速解密与签名过程的小技巧，本质上来说这是一种大数快速幂（取模）的算法，对于大数的乘法，无论采用何种算法（如 Karatsuba 或 FFT 等），其时间复杂度都不再能视作 O(1)，一般大数运算都会由密码学函数库提供.

计算 md(modN) 等价于解方程 (2)，显然有解

x≡md(modpq)

由于 p,q 是素数，它们显然互素，即 gcd(p,q)=1. 根据 CRT 的表述，方程 (2) 能拆开写成方程组 (3) 并拥有相同解集.

{x≡md(modp)x≡md(modq)

通过这样做，模 N:=pq 在位数上已经被劈开分成了 p,q，自然地为 d 的降幂提供了机会.

对于一个素数，它的 Carmichael 函数值与 Euler 函数值相同，即

λ(p)=φ(p)=p−1,λ(q)=φ(q)=q−1

令 dp:≡d(modλ(p)) 与 dq:≡d(modλ(q))，即存在 kp,kq∈Z 使得

d=kpλ(p)+dp=kqλ(q)+dq,

通过应用 Euler 定理，整理得到降幂形式 (4)，

{x≡md≡mkpλ(p)+dp≡mdp(modp)x≡md≡mkqλ(q)+dq≡mdq(modq)

这些更小的指数 dp 和 dq 在之前的成分列表中叫做 exponent1 和 exponent2，在生成私钥时它们就已经算好这两个成分，并存储在私钥文件中.

根据 CRT 方程组的算法，解为 (5)

x≡mdq+q∗(mdp−mdq)q(modpq)

其中 q∗:≡q−1(modp)，在之前的成分列表中叫做 coefficient.

综上所述，那些额外的成分一般叫做 CRT 成分，如下所示：

  • exponent1（对应 prime1 p）定义为 dp:≡d(modλ(p)), where λ(p)=p−1
  • exponent2（对应 prime2 q）定义为 dq:≡d(modλ(q)), where λ(q)=q−1
  • coefficient 定义为 q∗:≡q−1(modp)

公钥成分#

使用 OpenSSL 将之前的私钥导出为公钥，并查看其成分：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

$ openssl rsa -in sample.key -pubout | openssl pkey -pubin -noout -text
writing RSA key
Public-Key: (512 bit)
Modulus:
    00:e8:b1:ea:27:bc:3a:a6:9f:53:48:24:9c:5a:9d:
    9e:64:af:12:3e:ae:db:46:f0:4d:99:55:61:fd:c2:
    c8:45:35:25:05:e6:7b:37:c0:cc:92:7a:45:c0:5b:
    01:a3:4c:4e:87:5b:70:48:62:05:2a:6e:c2:3a:6a:
    f0:07:92:61:ad
Exponent: 65537 (0x10001)

公钥成分是更加简单的，恰恰好好是 (N,e).

恢复密钥#

RSA 中的陷门保证了无法轻易从公钥恢复出私钥，除非知道了 RSA 模的分解式即 N=pq. 在现有的分解数据库 factordb 上寻找 RSA 模的分解式是一个不错的方法，但在大多数场合下很难奏效.

要是有人使用了 RSA-512 的密钥，攻击者利用 CADO-NFS 实现的 NFS 算法不花一个星期就能把 RSA 模分解出来.

分布式分解#

CADO-NFS 是一个完备的软件套装，其中就包含了用于分布式计算的中心服务端，这里是一些注意事项：

  • 无论是服务端还是客户端，要尽量使用相同的 Linux 发行版或者 Docker 镜像

    不然的话可能会遇到 glibc 的版本兼容性问题.

  • 在启动了 CADO-NFS 的服务端之后，需要留意会输出一段可供恢复分解进度的命令，如果服务端意外退出，可以使用该命令恢复到退出前的进度.

前置步骤#

  • 为了编译 CADO-NFS，除了常用的工具链外，还要安装 cmake 和 libgmp3-dev.

  • 下载 CADO-NFS 源代码 tarball后， 解压并进入目录.

  • 运行 make -j8 开始构建. (可以根据机器情况，调整这里的并发任务数)

  • 这个时候 ./cado-nfs.py 和 ./cado-nfs-client.py 应该可以用了.

  • 从公钥文件 pub.pem 获取 RSA 的模，从此处开始一些数字末尾被抹掉了.

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

    $ openssl pkey -pubin -in pub.pem -noout -text
Public-Key: (512 bit)
Modulus:
    00:bc:dd:6e:bc:57:ae:a2:be:7d:ad:70:8f:71:0a:
    80:86:3b:c5:18:f7:ab:4d:5e:bd:a5:64:b2:65:d2:
    7c:d9:4c:5e:e3:c3:bc:33:b7:60:30:98:bd:6d:c4:
    **:**:**:**:**:**:**:**:**:**:**:**:**:**:**:
    **:**:**:**:**
Exponent: 65537 (0x10001)
$ openssl rsa -pubin -in public.pem -noout -modulus 
Modulus=BCDD6EBC57AEA2BE7DAD708F710A80863BC518F7AB4D5EBDA564B265D27CD94C5EE3C3BC33B7603098BD6DC4****************REDACTED****************

    得到了十六进制表示，需要转为十进制，例如可以直接让 Python 输出数值

    1
2

    $ python -c "print(0xBCDD6EBC57AEA2BE7DAD708F710A80863BC518F7AB4D5EBDA564B265D27CD94C5EE3C3BC33B7603098BD6DC4****************REDACTED****************)"
9891661152720289911993780388856560399924301310754393756699908896661301299157403390541217712185535804***********************REDACTED***********************

服务端#

1
2
3
4

./cado-nfs.py 9891661152720289911993780388856560399924301310754393756699908896661301299157403390541217712185535804***********************REDACTED*********************** \
              server.ssl=no server.address=0.0.0.0 server.port=52600 server.whitelist=0.0.0.0/0 \
              tasks.workdir=$HOME/nfs-work \
              --server

客户端#

1

./cado-nfs-client.py --server=http://server:52600 --override -t 8

将这里的 server 改成服务器的地址，每台机器可调整 --override -t 8 的线程数，以提高分解过程的单机并行度.

结果#

最后的输出便是两个素数，可以看下面的图.

95488332303787905388806934005632272891519544646395*************************** 103590259815731432651796987187054092306262180182970***************************

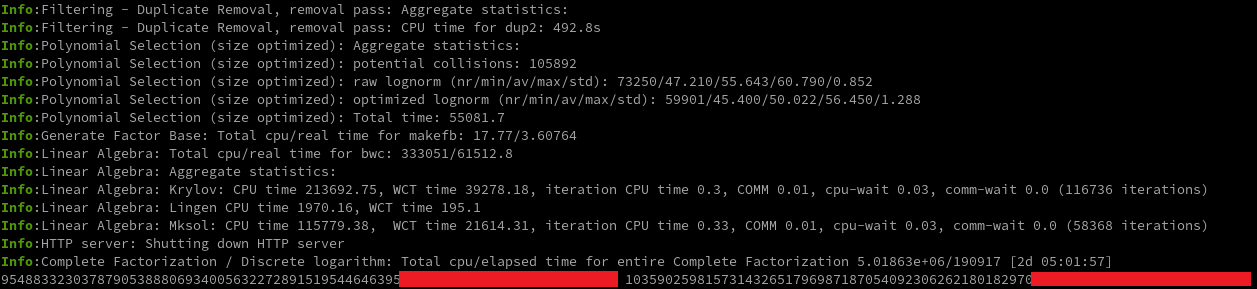
分解结果

恢复私钥#

为了更方便地基于 p,q,n,e 创建私钥，此处推荐 rsatool.py 这个工具，下载对应仓库并解压后，在目录中运行 pip install . 即可安装相关依赖.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

$ python rsatool.py -n 9891661152720289911993780388856560399924301310754393756699908896661301299157403390541217712185535804***********************REDACTED*********************** \
                    -p 95488332303787905388806934005632272891519544646395*************************** \
                    -q 103590259815731432651796987187054092306262180182970*************************** \
                    -e 65537 \
                    -f PEM -o recovered.key
Using (p, q) to calculate RSA paramaters

n =
bcdd6ebc57aea2be7dad708f710a80863bc518f7ab4d5ebda564b265d27cd94c5ee3c3bc33b76030
********************redacted********************

e = 65537 (0x10001)

d =
5d9b5a611b0c41392ccd23b6d48e21f965f26057909dbe513c825631454bffde921bc51a076cc3a5
********************redacted********************

p =
d31c7b17003dec91c9709546264c76c94670a4a9********redacted********

q =
e506026099230459a9a042fac22b258da1c43647********redacted********

Saving PEM as recovered.key

便得到了恢复的私钥 recovered.key，值得注意的是，该工具生成的私钥格式为 PKCS#1，可以转换成 PKCS#8 格式，只需运行

1

$ openssl pkey -in recovered.key